Definizione. I numeri formano un sistema completo di residui modulo se qualsiasi intero è modulo paragonabile a uno e solo uno di questi numeri.

Qualsiasi sistema completo di residui modulo è costituito da numeri che sono modulo incomparabili a coppie.

Teorema. Sia un sistema completo di residui modulo. Sia un intero coprimo a . Quindi - anche un sistema completo di residui modulo.

Prova.È necessario dimostrare che questi numeri sono incomparabili a coppie in modulo. Supponiamo il contrario. Permettere

Dal GCD, ciò che contraddice la condizione.

Teorema. Sia un sistema completo di residui modulo. Lascia che sia un numero intero. Quindi - anche un sistema completo di residui modulo.

Lemma. Se , allora GCD GCD .

Prova.

– un numero intero.

Da qui. Qualsiasi divisore comune è un divisore. Quindi MCD MCD.

Definizione. I numeri formano un sistema ridotto di residui modulo se sono coprimi to e qualsiasi intero coprimo to è paragonabile a uno e uno solo di questi numeri modulo.

Esempio. Il dato sistema di detrazioni modulo 10: 1,3,7,9.

Lemma. Tutti i suddetti sistemi di residui modulo consistono dello stesso numero di numeri, che sono indicati dalla funzione di Eulero.

Prova. Infatti, esistono due sistemi ridotti di residui modulo costituiti da diversi numeri di numeri:

Allora, poiché i numeri formano un sistema ridotto di residui modulo , ciascuno dei numeri è paragonabile a uno e uno solo di questi numeri. Poiché , allora, secondo il principio di Dirichlet, almeno due numeri da saranno paragonabili a un certo numero, e quindi saranno paragonabili tra loro in modulo. E questo contraddice il fatto che il dato sistema di residui modulo è . Significa, .

Proviamolo ora. Infatti, i numeri più piccoli e relativamente primi formano un sistema ridotto di residui modulo. Ciò segue dal lemma.

Definizione. La funzione di Eulero (o totiente) denota il numero di numeri inferiori e relativamente primi a .

Teorema. Se è un sistema di residui a modulo ridotto ed è un numero coprimo con , allora è anche un sistema a modulo ridotto di .

Se - semplice, allora .

Lemma. Se - semplice, allora .

Prova. In effetti, ci sono solo .

Lemma. Lasciamo che GCD. Poi . La funzione di Eulero è moltiplicativa.

Prova. Scriviamo tutti i numeri da 1 a come segue:

I numeri in ciascuna riga formano un sistema completo di residui modulo. Ciò significa che . è coprimo con tra loro. Inoltre, questi numeri sono disposti in colonne, uno sotto l'altro, poiché ogni colonna contiene numeri comparabili in modulo.

I numeri in ciascuna colonna formano un sistema modulo completo di residui. Infatti, l'esima colonna si ottiene se prendiamo i numeri che formano un sistema completo di residui modulo, li moltiplichiamo per un numero coprimo con e facciamo la somma a ciascuno di essi.

Pertanto, ciascuna colonna contiene esattamente numeri che sono primi rispetto a .

Poiché un numero sarà coprimo con c se e solo se è coprimo con e coprimo con , allora il numero di numeri coprimi con c è uguale a .

Teorema. Permettere

Scomposizione canonica di un numero. Poi

Prova. Dal lemma sulla molteplicità della funzione Eulero

Esempio.

Teorema (Eulero). Se e sono numeri relativamente primi, allora

Sia un sistema ridotto di residui modulo. . Allora è anche un sistema ridotto di residui modulo. Di conseguenza, ciascuno dei numeri della prima sequenza è paragonabile a uno dei numeri della seconda sequenza modulo , e ciascuno dei numeri della seconda sequenza è paragonabile a uno dei numeri della prima sequenza. Poi

Poiché ciascuno dei numeri è primo rispetto a , il confronto può essere ridotto a essi:

Conseguenza. Sia i numeri interi e i numeri naturali. Se , , mcd , allora .

Prova. Permettere . Poiché , allora è un numero naturale. Poi

Significa, .

88domanda
Omotetà e somiglianza dello spazio

Omotezia con centro O e coefficiente K denota Hk0

Le proprietà delle trasformazioni di omotetà e somiglianza dello spazio sono simili alle proprietà di omotetà e somiglianza di un piano, quindi lo studio della prima dovrebbe iniziare con una ripetizione della seconda. Similitudine dello spazio con coefficiente K può essere scomposto in una composizione di movimento e omotetà con un certo centro e lo stesso coefficiente.

Gli studenti dovrebbero sapere che con una tale trasformazione dello spazio, la grandezza dell'angolo (piano e diedro) viene preservata, linee rette e piani paralleli (perpendicolari) vengono mappati su linee rette e piani paralleli (perpendicolari). Ciò significa che con una tale trasformazione dello spazio, l'immagine di qualsiasi figura è una figura che ha la stessa forma della figura data, ma differisce da essa solo “per le sue dimensioni”.

Problema 12. Dato un tetraedro regolare RAVS; punti R 1 , UN 1 , IN 1 , CON 1 - centri delle sue facce (Fig. 14). Dimostrare che il tetraedro R 1 UN 1 IN 1 CON 1 è simile ad un tetraedro RAVS; trovare il coefficiente di questa somiglianza.

Soluzione. Lasciamo i punti N E K- rispettivamente al centro delle costole AB E Sole tetraedro RAVS, punto UN 1 - centro del viso RVS, punto R 1 - centro del viso ABC(Fig. 14). Significa che

RA 1: UN 1 K = AR 1: R 1 K = 2: 1,

UN 1 K : RK = R 1 K : AK = 1: 3,

Allo stesso modo, lo si può dimostrare
A1B1: AB= 1:3 e A1B1 AB,
A1C1 : AC= 1:3 e A1C1 AC,
B1C1 : Sole= 1:3 e B1C1 Sole,
B1R1 : realtà virtuale= 1:3 e B1R1 realtà virtuale,
S1R1 : SR= 1:3 e S1R1 SR.
Da queste relazioni tra i bordi dei tetraedri RAVS E P1A1B1C1 ne consegue che il tetraedro P1A1B1C1- corretto, quindi questi tetraedri sono simili; il coefficiente di somiglianza è 1/3. (In classi specializzate vale la pena dimostrare che questi tetraedri sono omotetici.)
Si può inserire la definizione: “Figura F1 chiamato figurativo F, se esiste una trasformazione di similarità spaziale che mappa la figura F alla figura F1" Quindi per dimostrare la somiglianza della figura F1 figura Fè sufficiente trovare almeno una trasformazione di somiglianza che la figura F viene visualizzato su una figura F1..

Definizione. La traslazione parallela, o, in breve, la traslazione di una figura, è la sua visualizzazione in cui tutti i suoi punti sono spostati nella stessa direzione di uguali distanze, cioè nel trasferire ciascuno due punti X e Y della figura, tali punti X" e Y" vengono associati in modo tale che XX" = YY"

La proprietà principale del trasferimento:

Il trasferimento parallelo preserva le distanze e le direzioni, ad es. X"Y" = XY

Ne consegue che il trasferimento parallelo è un movimento che conserva la direzione e viceversa un movimento che conserva la direzione è un trasferimento parallelo

Da tali affermazioni risulta inoltre che la composizione dei trasferimenti paralleli costituisce un trasferimento parallelo

La traslazione parallela di una figura viene specificata specificando una coppia di punti corrispondenti. Ad esempio, se viene specificato a quale punto A" va un dato punto A, allora questo trasferimento viene specificato dal vettore AA", e ciò significa che tutti i punti vengono spostati dallo stesso vettore, cioè XX" = AA" per tutti i punti X

Simmetria centrale

Definizione

I punti A e A" si dicono simmetrici rispetto al punto O se i punti A, A", O giacciono sulla stessa retta e OX = OX". Il punto O è considerato simmetrico a se stesso (rispetto a O)

Due figure si dicono simmetriche rispetto al punto O se per ogni punto di una figura esiste un punto dell'altra figura che è simmetrico rispetto al punto O e viceversa

Come caso speciale, una figura può essere simmetrica a se stessa rispetto a un certo punto O. Quindi questo punto O è chiamato centro di simmetria della figura, e la figura è centralmente simmetrica

Definizione

La simmetria centrale di una figura rispetto ad O è una mappatura di questa figura che associa ciascuno dei suoi punti ad un punto simmetrico rispetto ad O

Proprietà principale: la simmetria centrale preserva la distanza, ma inverte la direzione. In altre parole, due punti qualsiasi X e Y della figura F corrispondono ai punti X" e Y" tali che X"Y" = -XY

Prova. Supponiamo che, con simmetria centrale con il centro nel punto O, i punti X e Y siano mappati su X" e Y". Allora, come risulta dalla definizione di simmetria centrale, OX" = -OX, OY" = -OY

Allo stesso tempo, XY = OY - OX, X"Y" = OY" - OX"

Pertanto abbiamo: X"Y" = -OY + OX = -XY

Ne consegue che la simmetria centrale è un movimento che cambia direzione in senso contrario e viceversa, il movimento che cambia direzione in direzione opposta è simmetria centrale

La simmetria centrale di una figura viene specificata specificando una coppia di punti esistenti: se il punto A è mappato su A", allora il centro di simmetria è il punto medio del segmento AA"

Ruota attorno ad una linea retta

Per avere un'idea più chiara della rotazione attorno ad una retta occorre ricordare la rotazione su un piano in prossimità di un dato punto. Una rotazione su un piano attorno ad un dato punto è un movimento in cui ciascun raggio proveniente da un dato punto ruota dello stesso angolo nella stessa direzione. Passiamo ora alla rotazione nello spazio

Definizione. Rotazione di una figura attorno alla linea a di un angolo (si chiama mappatura tale che in ciascun piano perpendicolare alla linea a, si verifica una rotazione attorno al punto della sua intersezione con la linea a con lo stesso angolo (nella stessa direzione. La linea a è chiamato asse di rotazione e l'angolo è l'angolo di rotazione)

Da qui vediamo che la rotazione è sempre specificata dall'asse, dall'angolo e dal senso di rotazione

Teorema 1. La rotazione attorno ad una retta preserva le distanze, cioè è un movimento

Teorema 2. Se il movimento dello spazio ha una linea retta con il suo insieme di punti fissi, allora è una rotazione attorno a questa linea retta

Trasformazioni piane

Classi di detrazione. Sistemi di detrazione

Brevi informazioni dalla teoria

Usando il teorema della divisione con resto, puoi dividere un insieme di numeri interi in un numero di classi. Diamo un'occhiata a un esempio. Permettere M = 6. Allora abbiamo sei classi di partizione dell'insieme degli interi modulo 6:

R = 1;

R = 2;

R = 3;

R = 4;

R = 5;

dove attraverso R indica il resto della divisione di un numero intero per 6.

Ricordiamo il teorema della divisione con resto:

Teorema: Dividere un numero per il numero , , con resto significa trovare una coppia di numeri interi Q E R, in modo tale che siano soddisfatte le seguenti condizioni: .

È facile dimostrarlo per qualsiasi numero intero UN e per i numeri è possibile anche la divisione con resto Q E R sono determinati in modo inequivocabile. Nel nostro esempio, il sistema completo di residui minimi non negativi è l'insieme (0, 1, 2, 3, 4, 5); sistema completo di residui minimi positivi – set (0, 1, 2, 3, 4, 5); un sistema completo di residui con il più piccolo valore assoluto – set (-2,-1, 0, 1, 2, 3); il sistema ridotto dei residui è l'insieme (1,5), poiché ; insieme di fattori

Un metodo per eseguire operazioni aritmetiche su determinati numeri interi si basa su semplici principi della teoria dei numeri. L'idea di questo metodo è che i numeri interi sono rappresentati in uno dei sistemi non posizionali, nel sistema delle classi residue. Vale a dire: invece delle operazioni sugli interi, operano con i resti della divisione di questi numeri in numeri primi preselezionati - moduli .

Molto spesso numeri scegliere da un insieme di numeri primi.

Permettere …, .

Poiché nell'anello degli interi vale il teorema della divisione con resto, cioè dove , allora l'anello Z, per definizione, è euclideo.

Pertanto, come numeri puoi scegliere i resti della divisione di un numero UN SU p i rispettivamente.

Il sistema dei residui consente di eseguire operazioni aritmetiche su un insieme finito di numeri senza oltrepassarne i limiti. Sistema completo di detrazioni modulo N- qualsiasi insieme di N modulo incomparabile a coppie N numeri interi. Di solito come un sistema completo di detrazioni modulo N vengono presi i residui non negativi più piccoli

Divisione di numeri interi UN E M risulta il quoziente Q e il resto R , tale che

un = m q + r, 0 R m-1. Resto R chiamato DEDUZIONE modulo ohm M.

Ad esempio, per M = 3 e per M =5 otteniamo:

un = m q + r, m = 3	un = m q + r, m = 5
0 = 3 + 0	0 = 5 + 0
1 = 3 + 1	1 = 5 + 1
2 = 3 + 2	2 = 5 + 2
3 = 3 + 0	3 = 5 + 3
4 = 3 + 1	4 = 5 + 4
5 = 3 + 2	5 = 5 + 0
6 = 3 + 0	6 = 5 + 1
7 = 3 + 1	7 = 5 + 2

Se il resto è zero ( R=0 ), poi lo dicono M divide UN completamente (o M multiplo UN ), che significa M UN e i numeri Q E M chiamati divisori UN . Ovviamente 1 UN E UN UN . Se UN non ha altri divisori tranne 1 E UN , Quello UN – numero primo, altrimenti UN chiamato numero composto. Il più grande divisore positivo D due numeri UN E M è chiamato massimo comun divisore (MCD) e denota d = (a,m). Se MCD (a,m)= 1 , Quello UN E M non hanno divisori comuni tranne 1 , e sono detti coprimi l'uno rispetto all'altro.

A ogni DEDUZIONE A r = 0, 1, 2,…, m-1 corrisponde a un insieme di numeri interi a, b,… Dicono che i numeri sono uguali DEDUZIONE om sono comparabili in modulo e indicati con a b(mod m) o (a b) m.

Ad esempio, quando m = 3 :

Ad esempio, quando m = 5 :

Numeri UN , che sono comparabili in modulo M , formano una classe a parte DEDUZIONE R e sono definiti come un = m q+r.

Numeri UN chiamato anche CON DETRAZIONI modulo M . Non negativo DETRAZIONI un = r (A q=0 ), prendendo i valori dall'intervallo , formano un sistema completo di minimi residui modulo M.

DETRAZIONI UN , prendendo i valori dall'intervallo [-( ,…,( ] , A strano M o dall'intervallo [- A Anche M formano un sistema completo assolutamente più piccolo DEDUZIONE ov modulo M.

Ad esempio, quando M = si formano 5 classi di residui più piccoli

r = 0, 1, 2, 3, 4, a = -2, -1, 0, 1, 2. Entrambi gli insiemi di numeri dati formano sistemi completi deduzione ov modulo 5 .

Classe DETRAZIONI, i cui elementi sono coprimi rispetto al modulo M

detto ridotto. La funzione di Eulero determina quanto DETRAZIONI dal sistema completo delle deduzioni del modulo minimo M coprimo con M . Con semplice m=p abbiamo = p-1.

Definizione. L'insieme massimo di moduli incomparabili a coppie M numeri coprimi a M , chiamato dato sistema di detrazioni modulo M. Qualsiasi sistema ridotto di residui modulo M contiene elementi dove è la funzione di Eulero.

Definizione. Qualsiasi numero della classe di equivalenza єm chiameremo deduzione modulo ohm M. Totalità deduzione s, preso uno da ciascuna classe di equivalenza єm, è chiamato sistema completo deduzione ov modulo M(nel sistema completo deduzione ov, quindi, in totale M pezzi di numeri). I resti stessi quando divisi per M sono detti i più piccoli non negativi deduzione ami e, naturalmente, formano un sistema completo deduzione ov modulo M. Deduzione r si dice assolutamente piccolo se ïrï è il più piccolo tra i moduli deduzione ov di questa classe.

Esempio. Verifica se i numeri 13, 8, - 3, 10, 35, 60 formano un sistema completo di residui modulo m=6.

Soluzione: Per definizione, i numeri formano un sistema completo di residui modulo M, se ce ne sono esattamente m e sono incomparabili a coppie in modulo M.

L'incomparabilità a coppie può essere verificata sostituendo ciascun numero con il più piccolo residuo non negativo; se non ci sono ripetizioni, questo è un sistema completo di detrazioni.

Applichiamo il teorema della divisione con resto: un = m q+r.

13 = 6 2 + 1 13 1(mod 6); 8 = 6 1 + 2 8 2(mod 6);

3 = 6 (-1) + 3 -3 3(mod 6); 10 = 6 1 + 4 10 4(mod 6);

35 = 6 5 + 5 35 5(mod 6); 60 = 6 10 + 0 60 0(mod 6).

Abbiamo una sequenza di numeri: 1, 2, 3, 4, 5, 0, ce ne sono esattamente 6, non ci sono ripetizioni e sono incomparabili a coppie. Cioè formano un sistema completo di residui modulo m = 6.

Esempio. Sostituisci con il valore assoluto più piccolo e con il residuo positivo più piccolo 185 modulo 16.

Soluzione. Applichiamo il teorema della divisione con resto:

185 = 16 11 + 9 185 9(mod 16).

Esempio. Controlla se i numeri si formano (13, -13, 29, -9) sistema ridotto di residui modulo m=10.

Soluzione: Qualsiasi sistema ridotto di residui di modulo M contiene elementi dove è la funzione di Eulero. Nel nostro caso =4, perché tra i numeri naturali solo 1, 3, 7, 9 sono coprimi rispetto a 10 e non lo superano. Cioè, è possibile che questi quattro numeri costituiscano il sistema desiderato. Controlliamo la loro incomparabilità a coppie di questi numeri: =4, perché tra i numeri naturali solo 1, 3, 7, 9 sono coprimi con 10 e non lo superano. Cioè, è possibile che questi quattro numeri costituiscano il sistema desiderato. Controlliamo questi numeri per la loro incomparabilità a coppie: m .

Opzione 1. UN= 185, m = 12; Opzione 2. a = 84, m = 9;

Opzione 3. UN= 180, m = 10; Opzione 4. a = 82, m = 9;

Opzione 5. UN= 85, m = 11; Opzione 6. a = 84, m = 8;

Opzione 7. UN= 103, m = 87; Opzione 8. a = 84, m = 16;

Opzione 9. UN= 15, m = 10; Opzione 10. a = 81, m = 9;

Opzione 11. UN= 85, m = 15; Opzione 12. a = 74, m = 13;

Opzione 13. UN= 185, m = 16; Opzione 14. a = 14, m = 9;

Opzione 15. UN= 100, m = 11; Opzione 16. a = 484, m = 15;

Opzione 17. UN= 153, m = 61; Opzione 18. a = 217, m = 19;

Opzione 19. UN= 625, m = 25; Opzione 20. a = 624, m = 25;

Attività 3. Annotare il sistema completo e ridotto dei più piccoli

Clausola 17. Sistemi di detrazioni completi e ridotti.

Nel paragrafo precedente si è osservato che il rapporto єm comparabilità modulo arbitrario Mè una relazione di equivalenza sull'insieme degli interi. Questa relazione di equivalenza induce una partizione dell'insieme degli interi in classi di elementi equivalenti tra loro, cioè numeri che quando divisi per M equilibri identici. Numero di classi di equivalenza єm(gli esperti diranno: "indice di equivalenza єm") è esattamente uguale M .

Definizione. Qualsiasi numero della classe di equivalenza єm lo chiameremo residuo modulo M. Una serie di detrazioni prese una da ciascuna classe di equivalenza є m, è detto sistema completo di residui modulo M(nel sistema completo delle detrazioni, quindi, solo M pezzi di numeri). I resti stessi quando divisi per M sono chiamati i più piccoli residui non negativi e, ovviamente, formano un sistema completo di residui modulo M. Un residuo r si dice il più piccolo in assoluto se è il più piccolo tra i moduli dei residui di una data classe.

Esempio: Permettere M= 5. Poi:

0, 1, 2, 3, 4 - i più piccoli residui non negativi;

2, -1, 0, 1, 2 sono le detrazioni più piccole in assoluto.

Entrambi gli insiemi di numeri dati formano sistemi completi di residui modulo 5 .

Lemma 1. 1) Qualunque M pezzi non comparabili in modulo M i numeri formano un sistema completo di residui modulo M .

2) Se UN E M sono relativamente semplici e X M, quindi i valori della forma lineare ascia+b, Dove B- qualsiasi numero intero, anche percorrendo il sistema completo dei residui modulo M .

Prova. L'affermazione 1) è ovvia. Dimostriamo l'affermazione 2). Numeri ascia+b liscio M cose. Mostriamo che non sono comparabili in modulo M. Bene, lascia che sia per qualcosa di diverso x1 E x2 dal sistema completo di detrazioni si è scoperto che asse 1 +b є asse 2 +b(mod m). Quindi, secondo le proprietà dei confronti del paragrafo precedente, otteniamo:

asse 1 є asse 2 (mod m)

x 1 є x 2 (mod m)

- una contraddizione con il fatto che x1 E x2 sono diversi e presi dal sistema completo delle detrazioni.

Poiché tutti i numeri di una data classe di equivalenza є si ottengono da un numero di una data classe sommando un numero che è multiplo M, allora tutti i numeri di questa classe hanno modulo M lo stesso massimo comun divisore. Per alcuni motivi, di maggiore interesse sono quelle detrazioni che hanno con il modulo M massimo comun divisore uguale a uno, cioè residui coprimi rispetto al modulo.

Definizione. Il sistema ridotto delle detrazioni modulo Mè l'insieme di tutti i residui del sistema completo che sono coprimi rispetto al modulo M .

Il sistema ridotto viene solitamente scelto tra i residui non negativi più piccoli. È chiaro che il dato sistema di residui modulo M contiene j( M) pezzi di detrazioni, dove j ( M) – Funzione di Eulero – il numero di numeri inferiori a M e coprimo con M. Se a questo punto hai già dimenticato la funzione Eulero, guarda il paragrafo 14 e assicurati che lì sia stato detto qualcosa al riguardo.

Esempio. Permettere M= 42. Allora il sistema di residui dato è:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lemma 2. 1) Qualsiasi j ( M) numeri che sono incomparabili a coppie in modulo M e coprimo con il modulo, formano un sistema ridotto di residui modulo M .

2) Se (a,m) = 1 E X percorre il sistema ridotto dei residui modulo M, Quello ascia percorre anche il sistema ridotto dei residui modulo M .

Prova. L'affermazione 1) è ovvia. Dimostriamo l'affermazione 2). Numeri ascia sono incomparabili a coppie (questo è dimostrato allo stesso modo del Lemma 1 di questo paragrafo), ce ne sono esattamente j ( M) cose. È anche chiaro che tutti sono relativamente primi rispetto al modulo, perché (a,m)=1, (x,m)=1 Yu (ax.m)=1. Quindi i numeri ascia formare un sistema ridotto di residui.

Queste sono le definizioni e le proprietà fondamentali dei sistemi di residui completi e ridotti, tuttavia nel bagaglio delle conoscenze matematiche c'è tutta una serie di fatti molto interessanti e utili riguardanti i sistemi di residui. Se taci su di loro in questo paragrafo, temo che ciò costituirà una violazione diretta della legge della Federazione Russa sull'informazione, il cui occultamento dannoso è, secondo questa legge, un reato amministrativo e persino penale . Inoltre, senza la conoscenza di ulteriori importanti proprietà dei sistemi di detrazione, il paragrafo 17 risulterà molto scarno. Continuiamo.

Lemma 3. Permettere m1, m2, ..., mk– sono a coppie relativamente primi e m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, Dove

1) Se x1, x2,..., xk percorrere sistemi completi di residui modulo m1, m2, ..., mk di conseguenza, quindi i valori della forma lineare M1x1 +M2x2 + ...+Mkxk eseguire il sistema completo di detrazioni modulo m=m 1 m 2 ...m k .

2) Se x1, x2,..., xk percorrono i sistemi ridotti di residui modulo m1, m2, ..., mk di conseguenza, quindi i valori della forma lineare M1x1 +M2x2 + ...+Mkxk attraversano il sistema ridotto dei residui modulo m=m 1 m 2 ...m k .

Prova.

1) Forma M1x1 +M2x2 + ...+Mkxk ovviamente accetta m1m2...mk =m valori. Mostriamo che questi valori sono incomparabili a coppie. Bene, lascia che sia

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 С +M 2 x 2 С + ...+M k x k С (mod m)

Ogni sorta di cose Mj, diverso da SM, multiplo SM. Rimozione dei termini a sinistra e a destra nell'ultimo confronto che sono multipli SM, noi abbiamo:

M s x є M s x s С (mod m s) У x s є x s С (mod m s)

- una contraddizione con il fatto che xs attraversa il sistema completo dei residui del modulo SM .

2). Modulo M1x1 +M2x2 + ...+Mkxk ovviamente prende j ( m1) J ( m2) Ch ... Ch j ( m k) = j ( m 1 m 2 H ... H m k)= j ( M) (La funzione di Eulero è moltiplicativa!) di valori diversi, che si modulino a vicenda m=m 1 m 2 ...m k a coppie incomparabili. Quest'ultima è facilmente dimostrabile con un ragionamento simile a quello svolto nella dimostrazione dell'affermazione 1) di questo lemma. Perché ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 per ciascuno 1 ø s ø k, Quello ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, da qui l'insieme dei valori della forma M1x1 +M2x2 + ...+Mkxk forma un sistema ridotto di residui modulo M .

Lemma 4. Permettere x1, x2, ..., xk,x correre pieno, e x1, x2,..., xk, x– percorrere i sistemi di residui dati modulo m1, m2, ..., mk E m=m 1 m 2 ...m k rispettivamente, dove (m io m j)=1 A io No. j. Poi le frazioni (x 1 /m 1 +x 2 /m 2 +...+x k /m k) coincidono con le frazioni (x/m) e frazioni ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) coincidono con le frazioni (x/m) .

Prova. La dimostrazione di entrambe le affermazioni del Lemma 4 si ottiene facilmente applicando il precedente Lemma 3 dopo aver fornito ciascuna somma (x 1 /m 1 +x 2 /m 2 +...+x k /m k) E ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) ad un denominatore comune:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

Dove M j = m 1 ... m j-1 m j+1 ... m k .

Se ora teniamo conto che le parti frazionarie dei numeri si ottengono quando vengono divise per il modulo M due numeri qualsiasi comparabili in modulo M, sono uguali (sono uguali R/M, Dove Rè il più piccolo residuo non negativo di una data classe), allora le affermazioni di questo lemma diventano ovvie.

Nel resto di questa sezione accadrà la cosa più interessante: sommeremo le radici complesse M-esima potenza dall'unità, e scopriremo sorprendenti connessioni tra le somme di radici, i sistemi di residui e la già familiare funzione moltiplicativa di Möbius m ( M) .

Indichiamo con e k K esima radice M- oh potere dell'unità:

Ricordiamo bene queste forme di scrittura dei numeri complessi fin dal nostro primo anno. Qui k=0,1,...,m-1– percorre il sistema completo delle detrazioni modulo M .

Lascia che ti ricordi che l'importo e0 + e1 +...+ em-1 tutte le radici M l'esima potenza di uno è uguale a zero per qualsiasi M. Anzi, lasciamo e 0 + e 1 +...+ e m-1 =a. Moltiplichiamo questo importo per un numero diverso da zero e 1. Tale moltiplicazione geometrica nel piano complesso significa ruotare il corretto M-un triangolo con radici ai vertici e 0 , e 1 ,..., e m-1, con un angolo diverso da zero 2 p.m. È chiaro che in questo caso la radice e0 andrà alla radice e1, radice e1 andrà alla radice e2, ecc., e la radice em-1 andrà alla radice e0, cioè. somma e0 + e1 +...+ em-1 Non cambierà. Abbiamo e1a=a, Dove a=0 .

Teorema 1. Permettere m>0- numero intero, una O Z , X attraversa il sistema completo dei residui del modulo M. Allora se UN multiplo M, Quello

altrimenti, quando UN non un multiplo M ,

.

Prova. A UN multiplo M abbiamo: a=md E

A UN non divisibile per M, dividi numeratore e denominatore della frazione Sono SU D- massimo comun divisore UN E M, otteniamo una frazione irriducibile a 1/m 1. Quindi, per il Lemma 1, un 1x verrà eseguito attraverso il sistema completo di detrazioni modulo M. Abbiamo:

perché la somma di tutte le radici del grado m1 da uno è uguale a zero.

Lascia che ti ricordi che la radice e k M la esima potenza dell'unità si dice antiderivativa se il suo indice K coprimo con M. In questo caso, come è stato dimostrato nel primo anno, i diplomi successivi ek 1 , ek 2 ,..., ek m-1 radice e k formano l'intero insieme di radici M-esima potenza di uno o, in altre parole, e kè l'elemento generatore del gruppo ciclico di tutte le radici M-esimo potere dell'unità.

Ovviamente, il numero di diverse radici primitive M la esima potenza dell'unità è uguale a j ( M), dove j è la funzione di Eulero, poiché gli indici delle radici antiderivative formano un sistema ridotto di residui modulo M .

Teorema 2. Permettere m>0– un intero, x percorre il sistema di residui modulo ridotto M. Quindi (somma delle radici antiderivative di grado M):

dove m ( M) – Funzione di Möbius.

Prova. Permettere m=p 1 a 1 p 2 a 2 ...p k a k– espansione canonica di un numero M ; m1 =p1a1 , m2 =p2a2 , m3 =p3a3; x i percorre il sistema ridotto dei residui modulo io e io. Abbiamo:

A uns =1 si scopre che solo la radice e0 =1 non è antiderivativa, quindi la somma di tutte le radici antiderivative è la somma di tutte le radici meno uno:

quindi, se M libero da quadrati (cioè non divisibile per r2, A r >1), Quello

Se qualche indicatore COME maggiore di uno (es. M diviso per r2, A r>1), quindi la somma di tutte le radici antiderivative del grado SMè la somma di tutte le radici del grado SM meno la somma di tutte le radici non prime, cioè tutte le radici di un certo grado inferiore SM. Esattamente se m s = p s m s *, Quello:

Ora, cari lettori, dopo aver presentato alla vostra considerazione una quantità piuttosto significativa di informazioni sui sistemi di detrazioni completi e forniti, nessuno può accusarmi di aver violato maliziosamente la Legge della Federazione Russa sull'informazione nascondendola, quindi concludo questo paragrafo con soddisfazione.

I problemi

1 . Annotare su un pezzo di carta tutti i residui più piccoli non negativi e tutti i residui assolutamente più piccoli a) modulo 6, b) modulo 8. Subito sotto annota i sistemi di detrazione indicati per questi moduli. Disegna separatamente la sesta e l'ottava radice dell'unità sul piano complesso, cerchia le radici primitive in entrambi i disegni e trova la loro somma in ciascun caso. 2 . Permettere e– radice primitiva del grado 2n Da uno. Trova l'importo: 1+ e + e 2 +...+ e n-1 . 3 . Trova la somma di tutte le radici primitive: a) quindicesima; b) 24; c) la trentesima potenza di uno. 4 . Trova la somma di tutti i possibili prodotti delle radici primitive N-esima potenza da uno, presa a due a due. 5 . Trova l'importo K-x potenze di tutte le radici N-esimo potere dell'unità. 6 . Permettere m>1 , (a,m)=1 , B- numero intero, X percorre il sistema completo e x – ridotto dei residui del modulo M. Prova che: UN) B) 7 . Prova che: , Dove R attraversa tutti i fattori primi di un numero UN .

Clausola 17. Sistemi di detrazioni completi e ridotti.

Nel paragrafo precedente si è osservato che il rapporto є m comparabilità modulo arbitrario Mè una relazione di equivalenza sull'insieme degli interi. Questa relazione di equivalenza induce una partizione dell'insieme degli interi in classi di elementi equivalenti tra loro, cioè numeri che quando divisi per M equilibri identici. Numero di classi di equivalenza є m(gli esperti diranno: "indice di equivalenza є m") è esattamente uguale M .

Definizione. Qualsiasi numero della classe di equivalenza є m lo chiameremo residuo modulo M. Una serie di detrazioni prese una da ciascuna classe di equivalenza є m, è detto sistema completo di residui modulo M(nel sistema completo delle detrazioni, quindi, solo M pezzi di numeri). I resti stessi quando divisi per M sono chiamati i più piccoli residui non negativi e, ovviamente, formano un sistema completo di residui modulo M. Un residuo r si dice il più piccolo in assoluto se è il più piccolo tra i moduli dei residui di una data classe.

Esempio: Permettere M= 5. Poi:

0, 1, 2, 3, 4 - i più piccoli residui non negativi;

2, -1, 0, 1, 2 sono le detrazioni più piccole in assoluto.

Entrambi gli insiemi di numeri dati formano sistemi completi di residui modulo 5 .

Lemma 1. 1) Qualunque M pezzi non comparabili in modulo M i numeri formano un sistema completo di residui modulo M .

2) Se UN E M sono relativamente semplici e XM, quindi i valori della forma lineare ascia+b, Dove B- qualsiasi numero intero, anche percorrendo il sistema completo dei residui modulo M .

Prova. L'affermazione 1) è ovvia. Dimostriamo l'affermazione 2). Numeri ascia+b liscio M cose. Mostriamo che non sono comparabili in modulo M. Bene, lascia che sia per qualcosa di diverso x1 E x2 dal sistema completo di detrazioni si è scoperto che asse 1 +b є asse 2 +b(mod m). Quindi, secondo le proprietà dei confronti del paragrafo precedente, otteniamo:

asse 1 є asse 2 (mod m)

x 1 є x 2 (mod m)

- una contraddizione con il fatto che x1 E x2 sono diversi e presi dal sistema completo delle detrazioni.

Poiché tutti i numeri di una data classe di equivalenza є si ottengono da un numero di una data classe sommando un numero che è multiplo M, allora tutti i numeri di questa classe hanno modulo M lo stesso massimo comun divisore. Per alcuni motivi, di maggiore interesse sono quelle detrazioni che hanno con il modulo M massimo comun divisore uguale a uno, cioè residui coprimi rispetto al modulo.

Definizione. Il sistema ridotto delle detrazioni modulo Mè l'insieme di tutti i residui del sistema completo che sono coprimi rispetto al modulo M .

Il sistema ridotto viene solitamente scelto tra i residui non negativi più piccoli. È chiaro che il dato sistema di residui modulo M contiene j( M) pezzi di detrazioni, dove j ( M) – Funzione di Eulero – il numero di numeri inferiori a M e coprimo con M. Se a questo punto hai già dimenticato la funzione Eulero, guarda il paragrafo 14 e assicurati che lì sia stato detto qualcosa al riguardo.

Esempio. Permettere M= 42. Allora il sistema di residui dato è:

1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.

Lemma 2. 1) Qualsiasi j ( M) numeri che sono incomparabili a coppie in modulo M e coprimo con il modulo, formano un sistema ridotto di residui modulo M .

2) Se (a,m) = 1 E X percorre il sistema ridotto dei residui modulo M, Quello ascia percorre anche il sistema ridotto dei residui modulo M .

Prova. L'affermazione 1) è ovvia. Dimostriamo l'affermazione 2). Numeri ascia sono incomparabili a coppie (questo è dimostrato allo stesso modo del Lemma 1 di questo paragrafo), ce ne sono esattamente j ( M) cose. È anche chiaro che tutti sono relativamente primi rispetto al modulo, perché (a,m)=1, (x,m)=1 Yu (ax.m)=1. Quindi i numeri ascia formare un sistema ridotto di residui.

Queste sono le definizioni e le proprietà fondamentali dei sistemi di residui completi e ridotti, tuttavia nel bagaglio delle conoscenze matematiche c'è tutta una serie di fatti molto interessanti e utili riguardanti i sistemi di residui. Se taci su di loro in questo paragrafo, temo che ciò costituirà una violazione diretta della legge della Federazione Russa sull'informazione, il cui occultamento dannoso è, secondo questa legge, un reato amministrativo e persino penale . Inoltre, senza la conoscenza di ulteriori importanti proprietà dei sistemi di detrazione, il paragrafo 17 risulterà molto scarno. Continuiamo.

Lemma 3. Permettere m1, m2, ..., mk– sono a coppie relativamente primi e m 1 m 2 ...m k =M 1 m 1 =M 2 m 2 =...=M k m k, Dove

1) Se x1, x2,..., xk percorrere sistemi completi di residui modulo m1, m2, ..., mk eseguire il sistema completo di detrazioni modulo m=m 1 m 2 ...m k .

2) Se x1, x2,..., xk percorrono i sistemi ridotti di residui modulo m1, m2, ..., mk di conseguenza, quindi i valori della forma lineare attraversano il sistema ridotto dei residui modulo m=m 1 m 2 ...m k .

Prova.

1) Forma M1x1 +M2x2 + ...+Mkxk ovviamente accetta m1m2...mk =m valori. Mostriamo che questi valori sono incomparabili a coppie. Bene, lascia che sia

M 1 x 1 +M 2 x 2 + ...+M k x k є M 1 x 1 С +M 2 x 2 С + ...+M k x k С (mod m)

Ogni sorta di cose Mj, diverso da SM, multiplo SM. Rimozione dei termini a sinistra e a destra nell'ultimo confronto che sono multipli SM, noi abbiamo:

M s x є M s x s С (mod m s) У x s є x s С (mod m s)

- una contraddizione con il fatto che xs attraversa il sistema completo dei residui del modulo SM .

2). Modulo M1x1 +M2x2 + ...+Mkxk ovviamente prende j ( m1) J ( m2) Ch ... Ch j ( m k) = j ( m 1 m 2 H ... H m k)= j ( M) (La funzione di Eulero è moltiplicativa!) di valori diversi, che si modulino a vicenda m=m 1 m 2 ...m k a coppie incomparabili. Quest'ultima è facilmente dimostrabile con un ragionamento simile a quello svolto nella dimostrazione dell'affermazione 1) di questo lemma. Perché ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=(M s x s ,m s)=1 per ciascuno 1 ø s ø k, Quello ( M 1 x 1 +M 2 x 2 + ...+M k x k ,m s)=1, da qui l'insieme dei valori della forma M1x1 +M2x2 + ...+Mkxk forma un sistema ridotto di residui modulo M .

Lemma 4. Permettere x1, x2, ..., xk,x correre pieno, e x1, x2,..., xk, x– percorrere i sistemi di residui dati modulo m1, m2, ..., mk E m=m 1 m 2 ...m k rispettivamente, dove (m io m j)=1 A io No. j. Poi le frazioni coincidono con le frazioni (x/m) e frazioni coincidono con le frazioni (x/m) .

Prova. La dimostrazione di entrambe le affermazioni del Lemma 4 si ottiene facilmente applicando il precedente Lemma 3 dopo aver fornito ciascuna somma (x 1 /m 1 +x 2 /m 2 +...+x k /m k) E ( x 1 /m 1 + x 2 /m 2 +...+ x k /m k ) ad un denominatore comune:

(x 1 /m 1 +x 2 /m 2 +...+x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ;

( x 1 /m 1 + x 2 /m 2 +...+ x k /m k )=((M 1 x 1 +M 2 x 2 +...+M k x k)/m) ,

Dove M j = m 1 ... m j-1 m j+1 ... m k .

Se ora teniamo conto che le parti frazionarie dei numeri si ottengono quando vengono divise per il modulo M due numeri qualsiasi comparabili in modulo M, sono uguali (sono uguali R/M, Dove Rè il più piccolo residuo non negativo di una data classe), allora le affermazioni di questo lemma diventano ovvie.

Nel resto di questa sezione accadrà la cosa più interessante: sommeremo le radici complesse M il potere dell'unità, e scopriremo sorprendenti connessioni tra le somme di radici, i sistemi di residui e la già familiare funzione moltiplicativa di Möbius m ( M) .

Indichiamo con e k K esima radice M- oh potere dell'unità:

Ricordiamo bene queste forme di scrittura dei numeri complessi fin dal nostro primo anno. Qui k=0,1,...,m-1– percorre il sistema completo delle detrazioni modulo M .

Lascia che ti ricordi che l'importo e0 + e1 +...+ em-1 tutte le radici M l'esima potenza di uno è uguale a zero per qualsiasi M. Anzi, lasciamo e 0 + e 1 +...+ e m-1 =a. Moltiplichiamo questo importo per un numero diverso da zero e 1. Tale moltiplicazione geometrica nel piano complesso significa ruotare il corretto M-un triangolo con radici ai vertici e 0 , e 1 ,..., e m-1, con un angolo diverso da zero 2 p.m. È chiaro che in questo caso la radice e0 andrà alla radice e1, radice e1 andrà alla radice e2, ecc., e la radice em-1 andrà alla radice e0, cioè. somma e0 + e1 +...+ em-1 Non cambierà. Abbiamo e1a=a, Dove a=0 .

Teorema 1. Permettere m>0- numero intero, una O Z , X attraversa il sistema completo dei residui del modulo M. Allora se UN multiplo M, Quello

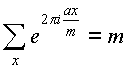
altrimenti, quando UN non un multiplo M ,

.

Prova. A UN multiplo M abbiamo: a=md E

A UN non divisibile per M, dividi numeratore e denominatore della frazione Sono SU D- massimo comun divisore UN E M, otteniamo una frazione irriducibile a 1/m 1. Quindi, per il Lemma 1, un 1x verrà eseguito attraverso il sistema completo di detrazioni modulo M. Abbiamo:

perché la somma di tutte le radici del grado m1 da uno è uguale a zero.

Lascia che ti ricordi che la radice e k M la esima potenza dell'unità si dice antiderivativa se il suo indice K coprimo con M. In questo caso, come è stato dimostrato nel primo anno, i diplomi successivi ek 1 , ek 2 ,..., ek m-1 radice e k formano l'intero insieme di radici M-esima potenza di uno o, in altre parole, e kè l'elemento generatore del gruppo ciclico di tutte le radici M-esimo potere dell'unità.

Ovviamente, il numero di diverse radici primitive M la esima potenza dell'unità è uguale a j ( M), dove j è la funzione di Eulero, poiché gli indici delle radici antiderivative formano un sistema ridotto di residui modulo M .

Teorema 2. Permettere m>0– un intero, x percorre il sistema di residui modulo ridotto M. Quindi (somma delle radici antiderivative di grado M):

dove m ( M) – Funzione di Möbius.

Prova. Permettere m=p 1 a 1 p 2 a 2 ...p k a k– espansione canonica di un numero M ; m1 =p1a1 , m2 =p2a2 , m3 =p3a3; x i percorre il sistema ridotto dei residui modulo io e io. Abbiamo:

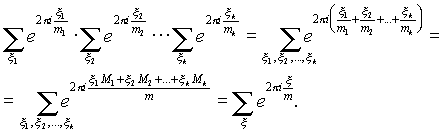
A uns =1 si scopre che solo la radice e0 =1 non è antiderivativa, quindi la somma di tutte le radici antiderivative è la somma di tutte le radici meno uno:

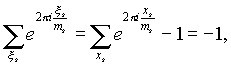
quindi, se M libero da quadrati (cioè non divisibile per r2, A r >1), Quello

Se qualche indicatore COME maggiore di uno (es. M diviso per r2, A r>1), quindi la somma di tutte le radici antiderivative del grado SMè la somma di tutte le radici del grado SM meno la somma di tutte le radici non prime, cioè tutte le radici di un certo grado inferiore SM. Esattamente se m s = p s m s *, Quello:

Ora, cari lettori, dopo aver presentato alla vostra considerazione una quantità piuttosto significativa di informazioni sui sistemi di detrazioni completi e forniti, nessuno può accusarmi di aver violato maliziosamente la Legge della Federazione Russa sull'informazione nascondendola, quindi concludo questo paragrafo con soddisfazione.

I problemi

1 . Annotare su un pezzo di carta tutti i residui più piccoli non negativi e tutti i residui assolutamente più piccoli a) modulo 6, b) modulo 8. Subito sotto annota i sistemi di detrazione indicati per questi moduli. Disegna separatamente la sesta e l'ottava radice dell'unità sul piano complesso, cerchia le radici primitive in entrambi i disegni e trova la loro somma in ciascun caso. 2 . Permettere e– radice primitiva del grado 2n Da uno. Trova l'importo: 1+ e + e 2 +...+ e n-1 . 3 . Trova la somma di tutte le radici primitive: a) quindicesima; b) 24; c) la trentesima potenza di uno. 4 . Trova la somma di tutti i possibili prodotti delle radici primitive N-esima potenza da uno, presa a due a due. 5 . Trova l'importo K-x potenze di tutte le radici N-esimo potere dell'unità. 6 . Permettere m>1 , (a,m)=1 , B- numero intero, X percorre il sistema completo e x – ridotto dei residui del modulo M. Prova che: UN) B) 7 . Prova che: , Dove R attraversa tutti i fattori primi di un numero UN .

Secondo la proprietà dei confronti n. 15, i numeri della stessa classe modulo M avere con il modulo M lo stesso GCD. Particolarmente importanti sono le classi per le quali è uguale a 1.

Prendendo un numero da ciascuna di queste classi, otteniamo sistema ridotto di detrazioni modulo M. Di solito è isolato dal sistema dei residui modulo meno non negativi M.

Sistema ridotto di residui modulo minimi non negativi M indicato con U M.

Il numero di numeri nel dato sistema modulo di residui M, ovviamente uguale a φ( M).

Esempio:

Il sistema di detrazioni modulo 15 dato è (1; 2; 4; 7; 8; 11; 13; 14). Si noti che φ(15)=(5–1)∙(3–1)= 8 e infatti, nel dato sistema di residui modulo 15 ci sono esattamente 8 elementi.

Dichiarazione 1

Qualsiasi φ( M) numeri che sono incomparabili a coppie in modulo M e coprimo con M, formano un sistema ridotto di residui.

(La dimostrazione è ovvia come nell’affermazione 1, punto 2)

Dichiarazione 2

Se ( UN, M) = 1, X percorre il sistema ridotto dei residui modulo M, Quello ascia percorre anche il sistema ridotto dei residui modulo M. (La dimostrazione è ovvia come nell'affermazione 2, punto 2).

Elemento inverso.

Dicono che l'elemento B chiamato inversione A UN modulo M, Se a∙b≡1(mod M), e scrivi B ≡ UN–1 (mod M).

In generale, la teoria classica dei numeri non ha bisogno di un concetto come elemento inverso, come si può vedere leggendo, ad esempio, . Tuttavia, la crittologia utilizza sistemi di residui sia negli aspetti teorici dei numeri che in quelli algebrici e quindi, per comodità di presentare i fondamenti algebrici della crittologia, introduciamo il concetto di elemento inverso.

La domanda sorge spontanea: è vero per tutti gli elementi di questo modulo? M esiste un inverso (per moltiplicazione), e se per alcuni elementi esiste l'inverso, come trovarlo?

Per rispondere a questa domanda utilizzeremo l’algoritmo euclideo esteso. Consideriamo innanzitutto i numeri coprimi UN e modulo M. Poi ovviamente ( UN,M)=1. L'algoritmo euclideo esteso consente di ottenere numeri X E sì, tale che ascia+mia=(UN,M), o, che è lo stesso, ascia+mia=1. Dall'ultima espressione otteniamo il confronto ascia+mia≡1(mod M). Perché il Mio≡0(mod M), Quello ascia≡1(mod M), che significa il numero ottenuto utilizzando l'algoritmo euclideo esteso Xè precisamente l'elemento inverso desiderato del numero UN modulo M.

Esempio.

UN=5, M=7. Ho bisogno di trovare UN-1 mod M.

Usiamo l'algoritmo euclideo esteso.

Inversione:

1=5–2∙2=5–(7–5∙1)∙2=5∙3–7∙2.

X=3, sì=–2.

5 -1 ≡3(mod 7)

Verifica: 5∙3=15. 15≡1(mod 7).

Infatti, 3 è l'inverso di 5 modulo 7.

Abbiamo quindi verificato costruttivamente che per i numeri coprimi ad un modulo esiste un inverso rispetto a tale modulo. Esistono elementi inversi per numeri che non sono coprimi rispetto al loro modulo?

Permettere ( UN,M)=D≠1. Allora a e m possono essere rappresentati nella forma UN=D∙UN 1 , M=D∙M 1 . Supponiamo che per a esista un elemento inverso modulo m, cioè B: UN∙B≡1(mod M). Poi UN∙b=m∙K+1. Oppure, qual è lo stesso, D∙UN 1 ∙b=d∙M 1 ∙K+1. Ma allora, secondo il Teorema 2 del §1 p.1, poiché sia ​​il membro sinistro di questa equazione che il primo termine del membro destro sono divisi in D, Quello D\1, ma questo non è vero, perché D≠1. Siamo arrivati ​​​​a una contraddizione, quindi l'ipotesi sull'esistenza dell'elemento inverso non è corretta.

Articoli simili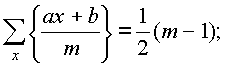